康托尔无穷大理论批判

数学研究情况简介

杨启宇

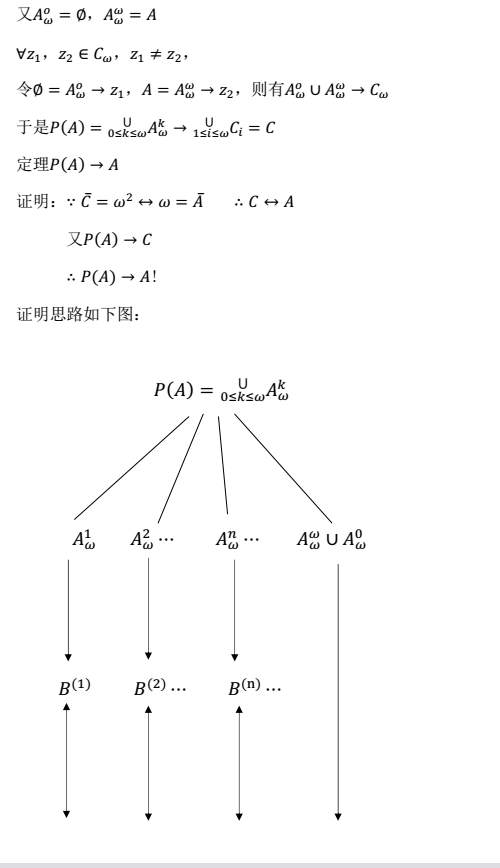
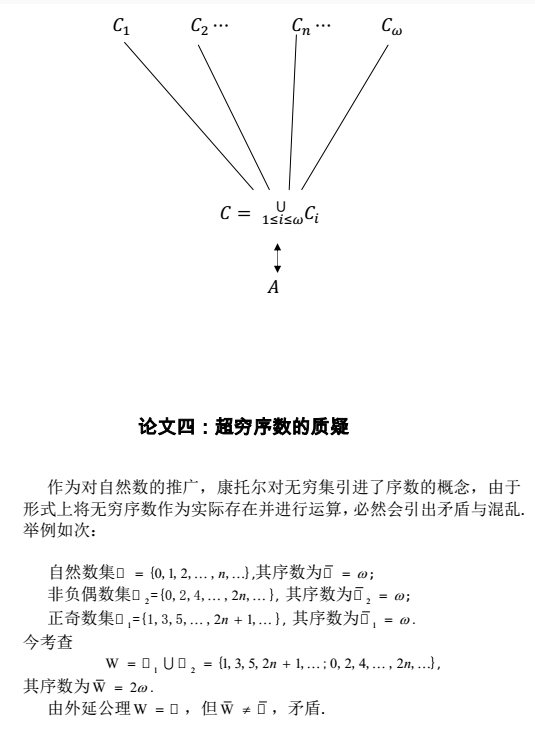
（中国国风网）康托尔创立的集合论经策墨罗、弗朗克尔公理化处理后，已成为当代主流数学界接受的经典数学基础。他的对角线法及用此方法证明的康托尔定理，更是有关无穷理论的奠基石。由此派生出著名的“连续统假设” 问题，在鼎鼎大名的“希尔伯特二十三大世界难题”榜上，高踞首位。笔者经过20年潜心思考，于2001年写出两篇文章：《关于无穷大基数的矛盾》与《关于无穷集与其幂集的一一对应》。第一篇文章分析康托尔对角线法推理中隐含“可将无穷个元素依次检验完毕”这样的前提。对此前提，康氏未给出证明，认为是不言而喻的。需要强调的是，笔者的文章不是从否认这一前提出发，而是从认同这一前提出发，却推出了相反的结果！从而揭示了对角线法本身的矛盾。第二篇文章只用一一对应法则，类似康托尔证明自然数集N与有理数集Q一一对应，直接建立起了无穷集A与其幂集P（A）间的一一对应。这就证明现有集合论无穷大理论不协调！当然，排名世界第一的难题“连续统假设”也就随之而“安乐死”。对现有集合论及建立在此基础上的现代数学来说，这两篇文章是毁灭性的！先将我的研究论文推出，也算我对数学界一个交代吧。

 责任编辑：孙克攀