
同学们,你相信吗?一个学习方法的掌握,让中等水平的学生都会解难题、竞赛题、奥数题,而且就在很短的时间里。再说,竞赛题能解,书上还有难题吗?
顾名思义,难题分解,当然是把难解的题分解。分解成容易的题, 基本概念题,一步头的题,一眼就看出来的题,人人都能做出来的题, 这应该是学习方法的重大突破。
下面我们通过实例,让每位读者相信这是真的,没有什么了不起, 让每位同学都能学会,掌握。最后分析该方法的奥秘、理论根据、实践结果,优缺点。
一个真实的例子
2014 年 10 月,沈阳市黄山路一个课后补习班上,十几个学生正在进行入学测试,他们大多来自北陵中学。一个老师拿出奥数竞赛题集,翻到应用题部分,第 24 题,让学生看,学生看过后,茫然不知所措的说:“我数学平均也就是 70 分,容易的题能做,难题不行,这奥数可比书上的难题还要难几倍。每次比赛,全班只有一个学生有资格参加,那是 100 分的学生,我们连想都不敢想。现在我们做不了, 我们还是走吧,不学了。
老师说:“稍等一会再走,你能读题吗?”学生说:“读当然行”,接着开始读。读了第一句,老师说:“停,想想,想到什么记下来”,学生记下第一个分析结果,老师又说:“再读”,第二句读完,老师又说“停,自己想”,学生又把想到结论记下来,接着第三句又重复这个过程,然后读第四句,又重复上面过程。老师说:“往下看”,学生一看,题目要求的答案已经作出了。
学生立即瞪大了眼睛:“怎么回事?我做出来了。”他又把书拿过来,看了又看,这真是奥数题集,我也能做奥数题,前后不过几分钟。另一个班,一个叫刘 XX 的女生,是光明中学优秀生,只是过去都在 90 分左右转,用新学习方法,三节课后就在100 分左右转。
XX 中学校长也带了学生来试验,完全成功。房地产老板李 XX 也带着孩子来试验,用新方法,几分钟,当场就把过去不会做的题做出来了。
芝加哥希林大学的数字老师 wendy 说:奥数题难就难在绕,绕了好几个弯子,学生就糊涂了,你把几个弯子分解了,成了几段直线, 解决了绕湾子,挺好。
二是这个方法对中等生、低等生也管用,这可是个大好事。当然, 对尖子生更有用
这里有什么决窍吗?怎么普及?
要说一点技巧没有,也不对,但是揭开之后,肯定不难,想想看, 中等水平学生几分钟就行,能有多难?
好,我们也不想卖关子,现在就一齐揭秘。
从学习方法上讲,也就是大家都知道的,‘一步一步分析法’。过去,大家都知道,这种方法很有用,但是谁也不敢保证,它肯定能解出来任何难题,竞赛题,更没有把握解奥数题。对这种方法的研究, 仅仅停留在初始阶段,一般深度,解决的问题很有限,作用有限。
今天同样的方法,我们都让中等水平的学生解书上难题,竞赛题,一些奥数题,而且当场试,几分钟见效果。肯定与过去的 ‘一步一步分析法’有区别,显然这里面还有一点奥秘,那就是,它增加了一些具体方法,细节方法,方法的延伸,就是这个延伸部分,却产生了神奇的效果。目前,用这种方法,奥数题集已解绍很多if,少数高难度题可能还要加强训练,但也有望解决,至于书上的题,还没出现困难。可以说,该方法成了解难题的关键。
下面通过录像讲解一遍(附文字说明)
(如果是成人读者,对小学分数除法概念记不清,请花 2 分钟温习一下,以便完全体会这种方法的神奇作用:一包苹果的1 /2是 5 公个斤,这包苹果有多重?你可能 5 秒钟算出来,10 公斤,那么请写出算式,稍微停 10 秒,你可以写出:5÷ 1/2 =10 公斤;好,请问:一包苹果的1/5 是5 ㎏,(Kg:公斤)这包苹果有多重?你会说 25 ㎏,你应该可以写出:5÷1/5=25㎏。好,再来一句巩固一下:一包苹果的2/5是 5 ㎏,这包苹果有多重?请写出算式,口算有点难,但是还是能写出:5÷2/5=5×5/2=12.5 ㎏)
下面同学们请看题:请开始,看着手表什计算时间
小红用三天看完一本书,第一天看完了全书的1/3,第二天看了余下的2/5,已知第二天比第三天少看 24 页,这本书共有多少页?
学生一看完,似乎有点想法,但又有点糊涂,毕竟是平均 70 分的学生, 呆呆的不知从那下手。
老师说:“读”,学生读完一句,老师说:“停,把想到的写下来。”学生写了“三天读一本书”,老师说“再读”,学生读第二句,老师说 “停,看看能想出什么,把所有能想到的都记下来”,学生写:第一天1/3,又想想,又写下:剩下二天读的(1-1/3=2/3)是2/3,老师说“再读一句”,“再想”,学生读了第三句“第二天看余下的2/5",思考一下,我已经找到余下是2/3, 第二天读的,当然是剩下两天2/3的2/5,写上2/3×2/5=4/15,学生正要往下读,老师阻止了他,“不急,再想想”
学生想想:第一天读1/3,第二日4/15,当然可以知道第三天的,写下:第三天可以求了,1-1/3-4/15=2/5,这也不难;老师说“不急,还可以想想吗?还会想出什么?”,学生看看,说:“每天读的都有了,没有了,没有什么了,还有什么,无非第三天2/5大,第一天1/3小,第二天4/15,好象更小,还有什么?无非每俩天可以相加,相减,有必要想这么多吗?”学生说“想不出来什么”,老师说“好,想到每两天可以相加,相减,很好,恐怕你没有想到,这个很简单的想法,非常容易的想法,似乎多余的想法,却是竞赛题的关键,请再读一句。” 当学生读到:“第二天比第三天少看 24 页”,老师说:别急,读到第二天比第三天少看……,停一停,不要读完,想想,’。学生只能又一次读到:“第二天比第三天少看……,”学生又说:我已知第三天2/5,第二天4/15, “那么第二天比第三天少看……,”两个数相减 2/5-4/15=2/15,这是两天读的差占全体比例,老师说“现在,读完这一句。”当学生读到:‘第二天比第三天少看 24 页”时,很兴奋,我刚刚已经求出来这两天的差 (占整体的比例)那么用 24页一除就行了。那么总数就有了,24÷2/15=180 老师说:“读。”当学生看最后一句时, 高兴的笑了:我已经做出来了。老师问:几分钟?学生回答:3 分 45 秒。
学生赶紧把教科书拿来,翻到封面,仔细看看,真是奥数题集, 老师问他,“我讲没讲数学定理?数学概念?”“没有”,“教你做题吗?” “没有”,是啊,就是“停、想想、”,这几个与数学不沾边的三个字,谁都会说;这个“停,想想、”三岁小孩也会说,整个过程就是简单的加减乘除,就是有个分数除法比较难,也不难,也是一步头的问题。已经做过很多分数除法练习了,死记硬背都知道了, 可是……可是用简单的加减乘除,居然作出奥数题,真是不可思议, 这个方法太容易,是不是从今以后,我能做难题、奥数题了?而且只用 3 分 45 秒!我是优秀生了?
旁边的学生也都说:“这有什么了不起,我也会了,我也能做奥数题了,我会了,会了,没有什么了不起。”
老师又提醒了一下:“且慢,不要骄傲,你入门了,总体方法有了,能解一批难题,视乎比过去聪明了,但是,还有一个‘但是’,还有一些细节、具体方法,你们没有完全掌握,再说,没有锻炼,不熟练, 要知道有时候细节也决定胜负。还要再练几周。”
现在看下一道题 (请看手表)
某工程队修一段路,第一天修了全长的1/5多 100 米,第二天修的比第一天的4/5多 20 米,第三天修 600 米,正好修完,这段公路全长是多少?
学生们看完题,又是一片茫然,刚才的狂劲消失了,只有两个85 分的学生开始一步一步分析、画图。当她们读了第二句:“第一天修了全长的1/5多 100 米”,画出了
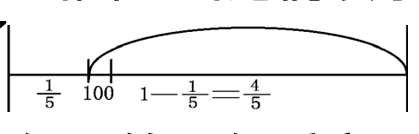
又写出 1-1/5=4/5(大弧线是全长的4/5,包括 100 米)但是第三句看完,久久下不了笔,说“老师,按你的办法也不行”。
老师笑笑:“首先你俩迈出重要的一步,知道一点一点分析,良好的开端,已经成功了一半,不过一点一点分析法,没有用准确。如果用准确,一定会成功。还有一点细节方法,方法的延伸,只要再多学习一点,可能会多解一大批题。”
“好,大家一齐来,还是老办法,读第一、二句,记下所想的。”大家读了两句,写出:第一天1/5,外加 100 米,1-1/5=4/5,但是在图中,100米是包含在4/5里面的。大家也都用图画出了
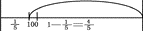
少数同学停一会,才把1/5剩下的4/5标出来。
老师:“继续读”,学生:“第二天比第一天的4/5多——”,老师赶紧插话:“停住”,“不许往下读”,“想想”。于是大家分析:第一天的4/5,第一天是1/5与 100 米,两个数f的4/5,又是比例,又是 100米,怎么办?一个学生说:第一天1/5的4/5好求,1/5×4/5=4/25,可是还有个100 米,它不是总数的比例,怎么办,这 100 米的4/5, 突然几个学生都说 100 米的4/5是 80 米,即 100 米×4/5=80 米,那么第一天1/5的4/5,就是1/5×4/5, 加 100 米×4/5=80 米。
“好”,老师说:“这里也就是把第一天的1/5和 100 米分开,一个一个解决,一个一个相乘,又是一个难题分解。”
“关键已经有了,把第一天的1/5与第一天的 100 米分开分析,饭要一口一口的吃,已知条件必须一个一个分析,特别是难题,千万不能把几个条件放在一起分析,奥数难就难在这里,如果一齐读完第三句,第三句有两个条件,4/5, 还有 20 米,与前面一句两个条件相结合,就是四个条件,放在一起,可以分析出非常多的结果,比较多的数据同时出现,一般同学就闷了,脑子就乱了,如果只读半句,只读一个条件,就开始分析,结合前面的已知条件分析,就容易得多,把第三句的半句中条件4/5当成一道题,结合前面的条件,认真分析,比较轻松;而且第一次只结合前一句的一个条件1/5分析,很容易,下一步,再把4/5结合第一天的100 米一起分析,还是简单的乘法;恰如一个重担,一个人挑不动,分两次,就容易了,这就是一个具体方法,方法的细节。’这就是难题分解, 把高难度的奥数题分解成简单的加减乘除。分解成普通学生都能解的题。可以看出,到现在为止,分解以后,都是简单的,一步就看出来的基本题。
“好,总结一下,这次你们就是‘按条件分析’,一点一点,先把第二句1/5与 100 米分开,同时把第三句的两个条件分开,4/5和2O米分开,先求1/5的4/5,可求,然后 100 米的4/5也可求,这里必须一点一点分析,千万不能一句一句分析;因为一句里有两个条件,第二句又有两个条件,四个条件一齐想是不可以的,不叫分解了,又叫大杂烩了。
好,记下来,现在可以看第三句的下半句了”下半句是“,,,,,,,4/5多20 米,现在不必考虑4/5了,只要求多2O米数就行了,看如下图:
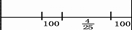 一一l 一一l
前面已经得出的结果 100×4/5=80 米,比 80 米多 20米是 100 米,又是一个 100 米,”老师说:“画上去”,”现在可以看下面一句’:‘第三天修 600 米’,也画上去”,看完第四句,也画上,看图想一想。

略停 10 秒,大多数同学都看出来了:1-1/5-4/25 所占全体的比例,就是 600+100+100 所占全体的比例,题目都明白了,当然也就做出来了。(600+100+100)÷(1-1/5-4/15)是总数。
这段时间是 6 分 40 秒,包括老师讲解、学生做题。
这一次,学生们不敢说什么都会了,只是问:还有什么细节方法
吗?看来,虚心、好学的习惯开始形成了。
理论
一.我们可以看到的是,分解法可以一句一句分解,也可以一个条件一个条件分解,这是细节,重要的细节。
为什么每一步要写下来?是,必须写,许多条件、有用的分析结果,在脑子里有个停留的过程,一秒不行,至少必须三秒,写下来需要三秒,如果在脑子里只停留一秒,容易忘记,等分析到了第三句,第四句,就记不清前面的分析洁结果了,如果忘记前面分析出来的任何一个结果,就可能解不出来。这是多次失败总结的教训。
二.“再想一下”这句话看来没什么,有人说‘我一次就想到了几个结果,用不着再想一下,实际上,90% 的学生需要再想,多数同学不能一步看出所有结果, 90 %的学生少了这个 再想几秒钟,该分析的没有全部分析出来, 就做不出来,就是好学生,有时也会少分析出一个结果,也是做不出来。”,所以细节也决定成败。要知道,解决占 90 %的中等水平学生,让他们成为优秀生,是多么重要,这是一个艰巨的任务,也是一个无比光荣的任务,仅仅只解决少数尖子生,意义不算大。
下面我们从理论上分析一下,这种方法的可靠性,可行性,可能的结果,还有多次的教训,以引起重视,达到效果,这样才可以彻底得到理论上的解决,将使你解决大量问题。
检验一个理论的完整,一个方法的可靠,也要看它是否解决多少问题。
首先我们要解的题都在课本的学习内容里,考大学不会考博士生学的定理,不可能超出中学课本这个范围。奥数也只能在这个范围里。书上定义、定律、公式会了,容易做的基本题应该会了,这时,如果学会难题分解,所有的难题都能分解成为容易做的简单题,那么各种题应该都能做,应该有这条路。
再者,所有要解的题目范围只能是: 学习过的定义、定理、公式的不同组合或者排列,这些定理、公式、定义(排列,组合的元素)、都在中学课本已知的定义、定理、公式里,超出去不可能的。
想把复杂的题——不同定义、定理、公式的排列组合,分解成它们原来的组成元素,肯定是可以的,必定有路的。分解之后就直接用定义定理解,它必定可以分解成一步头的、简单的题,基本概念题。只要上课听懂了的,中等水平甚至 60 分的,能做书上例题的,都可以做难题。
二、还是那个例子,一个人挑 200 斤不行,一般人都不行,如果把 200 斤分成 5 份,那么几乎每个人都能挑动一份,40 斤,只要掌握了分解的方法,人人都能解难题。一道题分解成5个简单题,这就是方法。
三、那位希林学院的老师看的很准,他说奥数题就是绕,绕了好几个弯子,学生不可能一步解出来,一眼看出来。
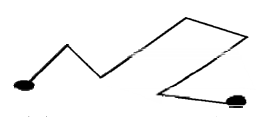
这个图从起点到终点,中间拐了六个弯子,不容易一眼就看到终点,一步看到结果, 但是,如果把六个弯子分解成六段直线,每段直线都是一眼能看出结果的题,都是直接用现成定理解的题,变成简单的四则运算,于是可解也。
四、正推为主,有人说倒背如流水平最高。我们不访试一下,倒背一个句子: 把‘某工程队修一段路’,倒过来:路段一修队程工某,你背背看?比顺背慢几倍?5 分钟以后还能记得吗?如果倒背一篇
文章,一天行吗?一天也不行,背完就全忘了,就没有头绪了,比顺着背难很多。
所以顺着推导,运算是轻松的,一步一步推出的结论,符合开始上课学习定理的过程,如果从结论倒推就累的多,做题也是,从一个个已知条件去分析,比较快;逆推有时可以用,但是尽量多用顺推, 符合学习的过程,比较容易。‘难题分解’着重顺着推导,大大减少难度。看题不要匆匆忙忙看完,一道题 3—5 个已知条件,每个条件又能分析出来几个结果,那么 3—5 个已知条件,就能得出十几个结果,这么多元素,同时堆在脑子里,好乱,难免丢掉 1—2 个,漏了一个结果就可能做不出来。
我们的难题分解,一个一个分析,就轻松的多,每一个条件都当成一道题,特别是第四个条件、第五个条件,一个条件必须当成一道题,认真分析,结合前面的每一个条件,结合前面的每一个结果,就可以把难题化解成容易的、简单题。如同剥洋葱,每剥一层,才能看到下一层,每分析一个条件,再能看到下一步道路。
如果把每一个已知条件都做为一道题,认真分析,记下结果,每次也就只分析出 2—4 个结果,不会漏掉,脑子不乱;再把结果放在一起,一对一对分析,所有结论都漏不掉,就容易解题;再说,分解以后,都是很容易的四则运算,每一步分析也就几秒钟。我们上面的分
如果怕考试时间不够,匆匆忙忙一气看完题,结果从最后一句求解去分析,成了逆推,增加了难度。快速看完题,短时间内,脑子里同时出现几个己知条件 十几个分析结果,那必然很乱,不可能清晰,失败的可能性很大。
疑难问题解答
每一步分析,可能有的结果用不着,但是不会漏,看来多用了十几秒,然而解一般难题,每一步十秒,一道题两分钟就是足可以解了。用过去的老式分析方法,也一定会分析出很多多余的结果,不比我们的方法省时间。通过多次实验,我们这种方法,解题速度不但不慢,反而很快,一般节省1/3 — 1/2 的时间。考试总是最早做完。
五、但是如果按过去的分析方法,匆匆忙忙看题,不小心漏掉一个分析结果,可能 10 分钟也做不出来。这才是真正耽误时间的地方, 所以不要担心一步一步分析会浪费时间,会分析多余的结果。实际上,每一步分析就是 5-10 秒,一道题 2-3 分钟就做出来了。
再说,没有做出来之前,无法判定那步分析是多余的。按过去的方法,一样必定会分析出一些多余的结果,这是解题过程必然发生的。当然一般性难题、不是很难的题,可以简单分析,对于奥数题、简单分析是不行的,只有细细分析。顺利做出来,反而是最快的。
配套方法
与本方法配套的分支方法还有几个,它们可以保证难题分解方法的实施。更重要的是,它们大大加快解题速度。
1、基本定理不懂,公式记不清,理解不深,怎么办?我们提供一套方法,叫‘融入数学体系法’,让你快速的记忆, 牢固的、准确的记忆。而且比较省时间。
2、粗心大意,似乎不是老师的责任,任何一步粗心,肯定得不了高分,解题过程中粗心,是解不下去的主要原因之一。
但是许多责任心强的老师会主动提出办法,帮助学生解决粗心, 我们针对各种粗心大意,提出解决的系统方法,包括一个个具体方法, 彻底解决粗心大意。定义为‘消除紧张法’,数据证明,我们这套方法,学生基本上不再粗心大意了。每次考试能增加 10—20 分。
3、预习,也就是自学,目前只有少数学生可以,老师提倡,但是多数学生做不到,或者匆匆预习,太肤浅,没达到要求。如何普及到每一个学生。让每个学生都会自学,包括读书的速度,预习的程序, 检查的标准,又是一套方法。
对不起,一篇文章太长了,我们下次再聊,我们将发表系列文章, 和大家一起探讨学习方法,欢迎同学们,老师们,朋友们来信,再见。

刘元澄先生
【作者简介】刘元澄,1945年5月25号出生,美籍华人,美国华尔街报记者兼办公室主任。安徽同乡会主席。
责任编辑:孙克攀
|
 | 设为首页 | 加入收藏 | 网站地图 | 活动报名/会员申报 | 证件查询 | 书画商城
| 设为首页 | 加入收藏 | 网站地图 | 活动报名/会员申报 | 证件查询 | 书画商城
网友点评